Blood, Sweat, and Buffers: pH Regulation During Exercise
Acid-Base Equilibria Experiment
Authors: Rachel Casiday and Regina Frey
Department of Chemistry, Washington University, St. Louis, MO 63130
Key Concepts:
- Exercise and how it affects the body
- Acid-base equilibria and equilibrium constants
- How buffering works
- Quantitative: Equilibrium Constants
- Qualitative: Le ChaTelier's Principle

How Does Exercise Affect the Body?
Many people today are interested in exercise as a way of improving their health and physical abilities. But there is also concern that too much exercise, or exercise that is not appropriate for certain individuals, may actually do more harm than good. Exercise has many short-term (acute) and long-term effects that the body must be capable of handling for the exercise to be beneficial. Some of the major acute effects of exercising are shown in Figure 1.
When we exercise, our heart rate, systolic blood pressure, and cardiac output (the amount of blood pumped per heart beat) all increase. Blood flow to the heart, the muscles, and the skin increase. The body's metabolism becomes more active, producing CO2 and H+ in the muscles. We breathe faster and deeper to supply the oxygen required by this increased metabolism. Eventually, with strenuous exercise, our body's metabolism exceeds the oxygen supply and begins to use alternate biochemical processes that do not require oxygen.
These processes generate lactic acid, which enters the blood stream. As we develop a long-term habit of exercise, our cardiac output and lung capacity increase, even when we are at rest, so that we can exercise longer and harder than before. Over time, the amount of muscle in the body increases, and fat is burned as its energy is needed to help fuel the body's increased metabolism.

Figure 1
This figure highlights some of the major acute (short-term) effects on the body during exercise.
Chemical Changes in the Blood During Exercise
In previous tutorials ("Hemoglobin and the Heme Group: Metal Complexes in the Blood for Oxygen Transport",
"Iron Use and Storage in the Body: Ferritin and Molecular Representations", "Maintaining the Body's Chemistry: Dialysis in the Kidneys") you learned about the daily maintenance required in the blood for normal everyday activities such as eating, sleeping, and studying. Now, we turn our attention to the chemical and physiological concepts that explain how the body copes with the stress of exercise. As we shall see, many of the same processes that work to maintain the blood's chemistry under normal conditions are involved in blood-chemistry maintenance during exercise, as well.
During exercise, the muscles use up oxygen as they convert chemical energy in glucose to mechanical energy. This O2 comes from hemoglobin in the blood. CO2 and H+ are produced during the breakdown of glucose, and are removed from the muscle via the blood. The production and removal of CO2 and H+, together with the use and transport of O2, cause chemical changes in the blood. These chemical changes, unless offset by other physiological functions, cause the pH of the blood to drop. If the pH of the body gets too low (below 7.4), a condition known as acidosis results. This can be very serious, because many of the chemical reactions that occur in the body, especially those involving proteins, are pH-dependent. Ideally, the pH of the blood should be maintained at 7.4. If the pH drops below 6.8 or rises above 7.8, death may occur. Fortunately, we have buffers in the blood to protect against large changes in pH.

How Chemicals Are Exchanged in the Body
All cells in the body continually exchange chemicals (e.g., nutrients, waste products, and ions) with the external fluid surrounding them (Figure 2). This external fluid, in turn, exchanges chemicals with the blood being pumped throughout the body. A dominant mode of exchange between these fluids (cellular fluid, external fluid, and blood) is diffusion through membrane channels, due to a concentration gradient associated with the contents of the fluids. (Recall your experience with concentration gradients in the "Membranes, Proteins, and Dialysis" experiment.) Hence, the chemical composition of the blood (and therefore of the external fluid) is extremely important for the cell. If, for instance, the pH of the blood and external fluid is too low (too many H+ ions), then an excess of H+ ions will enter the cell. As mentioned above, maintaining the proper pH is critical for the chemical reactions that occur in the body. In order to maintain the proper chemical composition inside the cells, the chemical composition of the fluids outside the cells must be kept relatively constant. This constancy is known in biology as homeostasis.
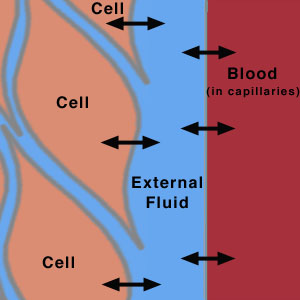
Figure 2
This is a schematic diagram showing the flow of species across membranes between the cells, the extracellular fluid, and the blood in the capillaries.
The body has a wide array of mechanisms to maintain homeostasis in the blood and extracellular fluid. The most important way that the pH of the blood is kept relatively constant is by buffers dissolved in the blood. Other organs help enhance the homeostatic function of the buffers. The kidneys help remove excess chemicals from the blood. It is the kidneys that ultimately remove (from the body) H+ ions and other components of the pH buffers that build up in excess. Acidosis that results from failure of the kidneys to perform this excretory function is known as metabolic acidosis. However, excretion by the kidneys is a relatively slow process, and may take too long to prevent acute acidosis resulting from a sudden decrease in pH (e.g., during exercise). The lungs provide a faster way to help control the pH of the blood. The increased-breathing response to exercise helps to counteract the pH-lowering effects of exercise by removing CO2, a component of the principal pH buffer in the blood. Acidosis that results from failure of the lungs to eliminate CO2 as fast as it is produced is known as respiratory acidosis.

Questions on Chemical Changes in Blood During Exercise and How Chemicals Are Exchanged in the Body
- Why does exercise generate H+?
- How can H+ generated in muscle cells during exercise affect the pH of the blood throughout the body (i.e., how does the concentration of H+ in the muscle cells affect the concentration of H+ in the blood)?

How Buffers Work: A Quantitative View
The kidneys and the lungs work together to help maintain a blood pH of 7.4 by affecting the components of the buffers in the blood. Therefore, to understand how these organs help control the pH of the blood, we must first discuss how buffers work in solution.
Acid-base buffers confer resistance to a change in the pH of a solution when hydrogen ions (protons) or hydroxide ions are added or removed. An acid-base buffer typically consists of a weak acid, and its conjugate base (salt) (see Equations 2-4 in the blue box, below). Buffers work because the concentrations of the weak acid and its salt are large compared to the amount of protons or hydroxide ions added or removed. When protons are added to the solution from an external source, some of the base component of the buffer is converted to the weak-acid component (thus using up most of the protons added); when hydroxide ions are added to the solution (or, equivalently, protons are removed from the solution; see Equations 8-9 in the blue box, below), protons are dissociated from some of the weak-acid molecules of the buffer, converting them to the base of the buffer (and thus replenishing most of the protons removed). However, the change in acid and base concentrations is small relative to the amounts of these species present in solution. Hence, the ratio of acid to base changes only slightly. Thus, the effect on the pH of the solution is small, within certain limitations on the amount of H+ or OH- added or removed.
The Carbonic-Acid-Bicarbonate Buffer in the Blood
By far the most important buffer for maintaining acid-base balance in the blood is the carbonic-acid-bicarbonate buffer. The simultaneous equilibrium reactions of interest are.
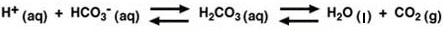
(1)
We are interested in the change in the pH of the blood; therefore, we want an expression for the concentration of H+ in terms of an equilibrium constant (see blue box, below) and the concentrations of the other species in the reaction (HCO3-, H2CO3, and CO2).
|
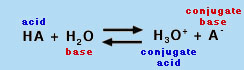
Recap of Fundamental Acid-Base Concepts An acid is a chemical species that can donate a proton (H+), and a base is a species that can accept (gain) a proton, according to the common Bronstead-Lowry definition. (A subset of the Bronstead-Lowry definition for aqueous solutions is the Arrhenius definition, which defines an acid as a proton producer and a base as a hydroxide (OH-) producer.) Hence, the conjugate base of an acid is the species formed after the acid loses a proton; the base can then gain another proton to return to the acid. In solution, these two species (the acid and its conjugate base) exist in equilibrium. Recall from this and earlier experiments in Chem 151 and 152 the definition of pH:
|
where [H+] is the molar concentration of protons in aqueous solution. When an acid is placed in water, free protons are generated according to the general reaction shown in Equation 3. Note: HA and A- are generic symbols for an acid and its deprotonated form, the conjugate base.
|
|
(3) |
Equation 3 is useful because it clearly shows that HA is a Bronstead-Lowry acid (giving up a proton to become A-) and water acts as a base (accepting the proton released by HA). However, the nomenclature H3O+ is somewhat misleading, because the proton is actually solvated by many water molecules. Hence, the equilibrium is often written as Equation 4, where H2O is the base:
|
|
(4) |
The Law of Mass Action and Equilibrium Constants
Using the Law of Mass Action, which says that for a balanced chemical equation of the type
|
|
(5) |
in which A, B, C, and D are chemical species and a, b, c, and d are their stoichiometric coefficients, a constant quantity, known as the equilibrium constant (K), can be found from the expression:
|
|
(6) |
where the brackets indicate the concentrations of species A, B, C, and D at equilibrium.
Equilibrium Constant for an Acid-Base Reaction
Using the Law of Mass Action, we can also define an equilibrium constant for the acid dissociation equilibrium reaction in Equation 4. This equilibrium constant, known as Ka, is defined by Equation 7:
|
|
(7) |
Equilibrium Constant for the Dissociation of Water
One of the simplest applications of the Law of Mass Action is the dissociation of water into H+ and OH- (Equation 8).
|
|
(8) |
The equilibrium constant for this dissociation reaction, known as Kw, is given by
|
|
(9) |
(H2O is not included in the equilibrium-constant expression because it is a pure liquid.) Hence, we can see that increasing the OH- concentration of an aqueous solution has the effect of decreasing the H+ concentration, because the product of these two concentrations must remain constant at a given temperature. Thus, in water, the equilibrium in Equation 8 underlies the equivalency of the Bronstead- "Lowry definition of a base (an H+ acceptor) and the Arrhenius definition of a base (an OH- producer).
To more clearly show the two equilibrium reactions in the carbonic-acid-bicarbonate buffer, Equation 1 is rewritten to show the direct involvement of water:
|
|
(10) |
The equilibrium on the left is an acid-base reaction that is written in the reverse format from Equation 3. Carbonic acid (H2CO3) is the acid and water is the base. The conjugate base for H2CO3 is HCO3- (bicarbonate ion). (Note: To view the three-dimensional structure of HCO3-, consult the Table of Common Ions in the Periodic Properties tutorial from Chem 151.) Carbonic acid also dissociates rapidly to produce water and carbon dioxide, as shown in the equilibrium on the right of Equation 10. This second process is not an acid-base reaction, but it is important to the blood's buffering capacity, as we can see from Equation 11, below.
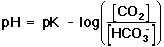 . . |
(11) |
The derivation for this equation is shown in the yellow box, below. Notice that Equation 11 is in a similar form to the Henderson-Hasselbach equation presented in the introduction to the Experiment (Equation 16 in the lab manual) Equation 11 does not meet the strict definition of a Henderson-Hasselbach equation, because this equation takes into account a non-acid-base reaction (i.e., the dissociation of carbonic acid to carbon dioxide and water), and the ratio in parentheses is not the concentration ratio of the acid to the conjugate base. However, the relationship shown in Equation 11 is frequently referred to as the Henderson-Hasselbach equation for the buffer in physiological applications.
In Equation 11, pK is equal to the negative log of the equilibrium constant, K, for the buffer (Equation 12).
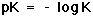 where K=Ka/K2 (from Equation 10). |
(12) |
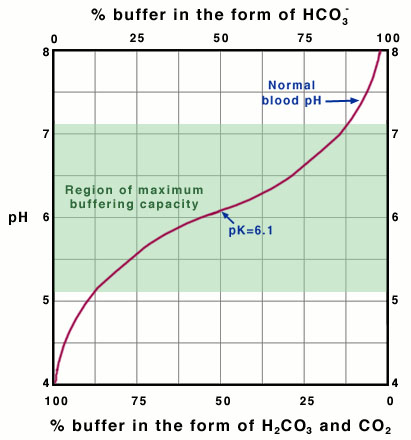
This quantity provides an indication of the degree to which HCO3- reacts with H+ (or with H3O+ as written in Equation 10) to form H2CO3, and subsequently to form CO2 and H2O. In the case of the carbonic-acid-bicarbonate buffer, pK=6.1 at normal body temperature.
|
Derivation of the pH Equation for the Carbonic-Acid-Bicarbonate Buffer We may begin by defining the equilibrium constant, K1, for the left-hand reaction in Equation 10, using the Law of Mass Action:
Ka (see Equation 9, above) is the equilibrium constant for the acid-base reaction that is the reverse of the left-hand reaction in Equation 10. It follows that the formula for Ka is
The equilibrium constant, K2, for the right-hand reaction in Equation 10 is also defined by the Law of Mass Action:
Because the two equilibrium reactions in Equation 10 occur simultaneously, Equations 14 and 15 can be treated as two simultaneous equations. Solving for the equilibrium concentration of carbonic acid gives.
Rearranging Equation 16 allows us to solve for the equilibrium proton concentration in terms of the two equilibrium constants and the concentrations of the other species:
Because we are interested in the pH of the blood, we take the negative log of both sides of Equation 17:
Recalling the definitions of pH and pK (Equations 2 and 12, above), Equation 18 can be rewritten using more conventional notation, to give the relation shown in Equation 11, which is reproduced below:
(19) |
As shown in Equation 11, the pH of the buffered solution (i.e., the blood) is dependent only on the ratio of the amount of CO2 present in the blood to the amount of HCO3- (bicarbonate ion) present in the blood (at a given temperature, so that pK remains constant). This ratio remains relatively constant, because the concentrations of both buffer components (HCO3- and CO2) are very large, compared to the amount of H+ added to the blood during normal activities and moderate exercise. When H+ is added to the blood as a result of metabolic processes, the amount of HCO3- (relative to the amount of CO2) decreases; however, the amount of the change is tiny compared to the amount of HCO3- present in the blood. This optimal buffering occurs when the pH is within approximately 1 pH unit from the pK value for the buffering system, i.e., when the pH is between 5.1 and 7.1.
However, the normal blood pH of 7.4 is outside the optimal buffering range; therefore, the addition of protons to the blood due to strenuous exercise may be too great for the buffer alone to effectively control the pH of the blood. When this happens, other organs must help control the amounts of CO2 and HCO3- in the blood. The lungs remove excess CO2 from the blood (helping to raise the pH via shifts in the equilibria in Equation 10), and the kidneys remove excess HCO3- from the body (helping to lower the pH). The lungs' removal of CO2 from the blood is somewhat impeded during exercise when the heart rate is very rapid; the blood is pumped through the capillaries very quickly, and so there is little time in the lungs for carbon dioxide to be exchanged for oxygen. The ways in which these three organs help to control the blood pH through the bicarbonate buffer system are highlighted in Figure 3, below
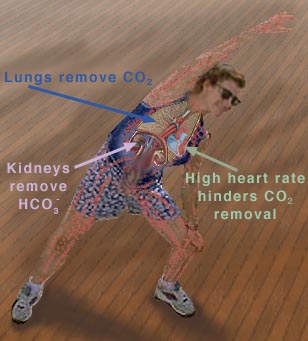
Figure 3 This figure shows the major organs that help control the blood
Removing CO2 from the blood helps increase the pH. |
Why the Optimal Buffering Capacity Is at pH=pK
Why is the buffering capacity of the carbonic-acid-bicarbonate buffer highest when the pH is close to the pK value, but lower at normal blood pH? The answer to this question lies in the shape of the titration curve for the buffer, which is shown in Figure 4, below.
Titration Curve for the Bicarbonate-Buffer System
It is possible to plot a titration curve for this buffer system, just as you did for your solution in the acid-base-equilibria experiment. In this plot, the vertical axis shows the pH of the buffered solution (in this case, the blood). The horizontal axis shows the composition of the buffer: on the left-hand side of the plot, most of the buffer is in the form of carbonic acid or carbon dioxide, and on the right-hand side of the plot, most of the buffer is in the form of bicarbonate ion. Note that as acid is added, the pH decreases and the buffer shifts toward greater H2CO3 and CO2 concentration. Conversely, as base is added, the pH increases and the buffer shifts toward greater HCO3- concentration (Equation 10).
|
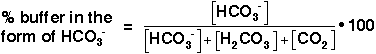
This is the titration curve for the carbonic
|
The slope of the curve is flattest where the pH is equal to the pK value (6.1) for the buffer. Here, the buffering capacity is greatest because a shift in the relative concentrations of bicarbonate and carbon dioxide produces only a small change in the pH of the solution. However, at pH values higher than 7.1, the slope of the curve is much higher. Here, a shift in the relative concentrations of bicarbonate and carbon dioxide produces a large change in the pH of the solution. Hence, at the physiological blood pH of 7.4, other organs must help to control the amounts of HCO3- and CO2 in the blood to keep the pH relatively constant, as described above.
Other pH-Buffer Systems in the Blood
Other buffers perform a more minor role than the carbonic-acid-bicarbonate buffer in regulating the pH of the blood. The phosphate buffer consists of phosphoric acid (H3PO4) in equilibrium with dihydrogen phosphate ion (H2PO4-) and H+. The pK for the phosphate buffer is 6.8, which allows this buffer to function within its optimal buffering range at physiological pH. The phosphate buffer only plays a minor role in the blood, however, because H3PO4 and H2PO4-are found in very low concentration in the blood. Hemoglobin also acts as a pH buffer in the blood. Hemoglobin protein can reversibly bind either H+ (to the protein) or O2 (to the Fe of the heme group), but that when one of these substances is bound, the other is released (as explained by the Bohr effect). During exercise, hemoglobin helps to control the pH of the blood by binding some of the excess protons that are generated in the muscles. At the same time, molecular oxygen is released for use by the muscles.

Questions on How Buffers Work: A Quantitative View
- If blood had a normal pH of 6.1 instead of 7.2, would you expect exercise to result in heavy breathing? Justify your answer.
- How would a graph like that found in Figure 4 differ for the phosphate buffer system?

Equilibrium Shifts: A Qualitative View
The above discussion treats changes in pH quantitatively. These changes in pH can be described qualitatively, also. A qualitative view is very useful for predicting how the pH will change in response to external conditions (such as exercise). The principle used for this qualitative view is known as Le Chatelier's Principle.
Le Chatelier's Principle
When a reactant or product of an equilibrium reaction is added to a solution that is at equilibrium, the added species will react to change the concentrations of the reactants and products in the solution until a new equilibrium is established (but the ratio of the concentrations given in the mass action expression (Equation 6) is the same, because the equilibrium constant, K, is a constant at a given temperature). This process is known as a shift in the equilibrium. In 1884, Henri Le Chatelier developed a rule to predict how a system in equilibrium will shift when the conditions of the system are changed. Although this rule can oversimplify the changes that occur in certain situations, it is a powerful and useful tool for predicting the direction of an equilibrium shift. Le Chatelier's Principle states that "if a change in conditions ([an external] 'stress') is imposed on a system at equilibrium, the equilibrium position will shift in a direction that tends to reduce that change in conditions" (Zumdahl, 208). For example, if the concentration of one of the products of an equilibrium reaction is increased in a solution that was at equilibrium (prior to the concentration increase), the equilibrium will shift so as to reduce the concentration of the product, i.e., more reactant will be generated. Of course, the reverse equilibrium shift would occur when the concentration of a product is decreased. The effect of a temperature change can also be predicted by Le Chatelier's Principle. (In the case of a change in temperature, the equilibrium constant actually changes.) If a reaction is exothermic, "heat" is treated as a "product" (e.g., A + B -> C + D + "heat"). If a reaction is endothermic, "heat" is treated as a "reactant" (e.g., "heat" + A + B -> C + D). Increasing the temperature can be thought of as increasing the amount of "heat" in the reaction. Examples of external stresses and the equilibrium shifts predicted by Le Chatelier's Principle are shown in the purple table below.
|
External Stress |
Predicted Equilibrium Shift |
| Change in pressure | Affects gases only. |
| Concentration of reactant(s) increased | Equilibrium shifts toward products (to the right). |
| Concentration of product(s) increased | Equilibrium shifts toward reactants to the left). |
| Temperature increased (exothermic reaction) |
Equilibrium shifts toward reactants (to the left). |
| Temperature increased (endothermic reaction) |
Equilibrium shifts toward products (to the right). |
Example: Removal of Bicarbonate by the Kidneys
Le Chatelier's Principle can be used to explain how the kidneys help prevent excessively high pH (a condition known as alkalosis). When the pH of the blood is too high, the kidneys remove bicarbonate ion (HCO3-) from the blood. As the kidneys decrease the blood's concentration of HCO3-, the equilibrium reaction in Equation 10 is shifted toward the left to compensate for the loss in HCO3-, according to Le Chatelier's Principle. When the equilibrium shifts to the left, more H+ ions are generated together with HCO3- ions. As a result, the pH decreases.

Questions on Equilibrium Shifts: A Qualitative View
- An emergency medical team evaluates an Olympic athlete and determines that she has alkalosis. What component of the carbonic-acid-bicarbonate buffer would the athlete be given to decrease the pH of the blood?
- Hyperventilation (very rapid and deep breathing, which reduces the concentration of CO2 in the blood) causes dizziness.
- How does hyperventilation affect the pH of the blood (i.e., is the pH increased or decreased as a result of hyperventilation)? Briefly, explain your answer in terms of equilibrium shifts.
- The normal first-aid treatment for hyperventilation is to have the patient breathe into a paper bag. Briefly, explain why this treatment works and tell what effect the paper-bag treatment has on the pH of the blood.

Summary: What Happens to the Blood During Exercise?
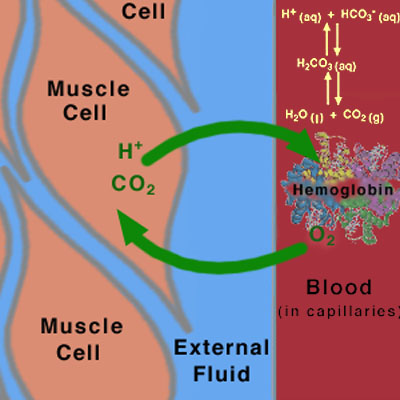
When you exercise, many of the processes that we have discussed in this and in previous tutorials work together to determine how the pH of the blood will change (Figure 5).
|
Figure 5
This diagram shows the diffusion directions for |
The following steps outline the processes that affect the buffers in the blood during exercise.
- Hemoglobin carries O2 from the lungs to the muscles through the blood.
- The muscles need more O2 than normal, because their metabolic activity is increased during exercise. The amount of oxygen in the muscle is therefore depleted in the muscles, setting up a concentration gradient between the muscle cells and the blood in the capillaries. Oxygen diffuses from the blood to the muscles, via this concentration gradient.
- The muscles produce CO2 and H+ as a result of increased metabolism, setting up concentration gradients in the opposite direction from the O2 gradient.
- The CO2 and H+ flow from the muscles to the blood, via these concentration gradients.
- The buffering action of hemoglobin picks up the extra H+ and CO2.
- If the amounts of H+ and CO2 exceed the capacity of hemoglobin, they affect the carbonic acid equilibrium (Equation 10), as predicted by Le Chatelier's Principle or the quantitative treatment in terms of equilibrium constants. As a result, the pH of the blood is lowered, causing acidosis.
- The lungs and kidneys respond to pH changes by removing CO2, HCO3-, and H+ from the blood.
Hence, the body has developed finely-tuned chemical processes (based on buffering and acid-base equilibria) that work in combination to handle the changes that exercise produces.

References:
Brown, Lemay, and Bursten.Chemistry: the Central Science, 7th ed. p. 631.
Vander, A. et al. Human Physiology, 6th ed. WCB McGraw-Hill, Boston, 1994, p. 463-466, 492-3, 552-6.
Zumdahl. Chem. Principles, 4th ed.p. 192-5, 208-214.

Acknowledgements:
The authors thank Dewey Holten, Michelle Gilbertson, Jody Proctor and Carolyn Herman for many helpful suggestions in the writing of this tutorial.
The development of this tutorial was supported by a grant from the Howard Hughes Medical Institute, through the Undergraduate Biological Sciences Education program, Grant HHMI# 71195-502005 to Washington University.
Copyright 1999, Washington University, All Rights Reserved.
Revised January 2001.

The statements enclosed herein have not been evaluated by the Food and Drug Administration. The products mentioned on this site are not intended to diagnose, treat, cure, or prevent any disease. Information and statements made are for education purposes and are not intended to replace the advice of your family doctor.






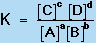
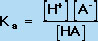
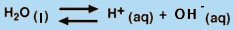
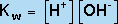 .
.
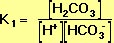 .
.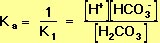 .
.
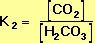 .
. .
.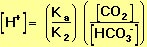 .
.
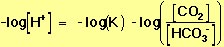 ,
,